3 Best Idle games for Teaching Math

Idle games are both intriguing and bewildering. Characterized by minimal player involvement and periods of inactivity, they seem to go against what is heralded as good game design, and yet have attracted a vast number of players. Let’s look at them in some more detail to see how they can be used to teach different mathematical concepts. 

What Makes an Idle Game?

An idle game can be defined as any game whose basic mechanism is to automatically generate a primary resource. This resource can then be spent on upgrades that increase the rate at which the resource is accrued. As the growth rate of accumulation increases, so does the cost of the upgrades at a slower pace. The core of idle games is usually all about finding a balance between production rates and production costs.

Throughout the game, costs tend to grow exponentially while production grows at a more linear rate. It is the loop of accumulation, reinvestment, and acceleration that defines the genre and distinguishes it from games that simply have an increasing score. The pinnacle of these games is that they are low effort and high reward, which could be the key to teaching mathematical ideas.

Determining the Most Efficient Purchase

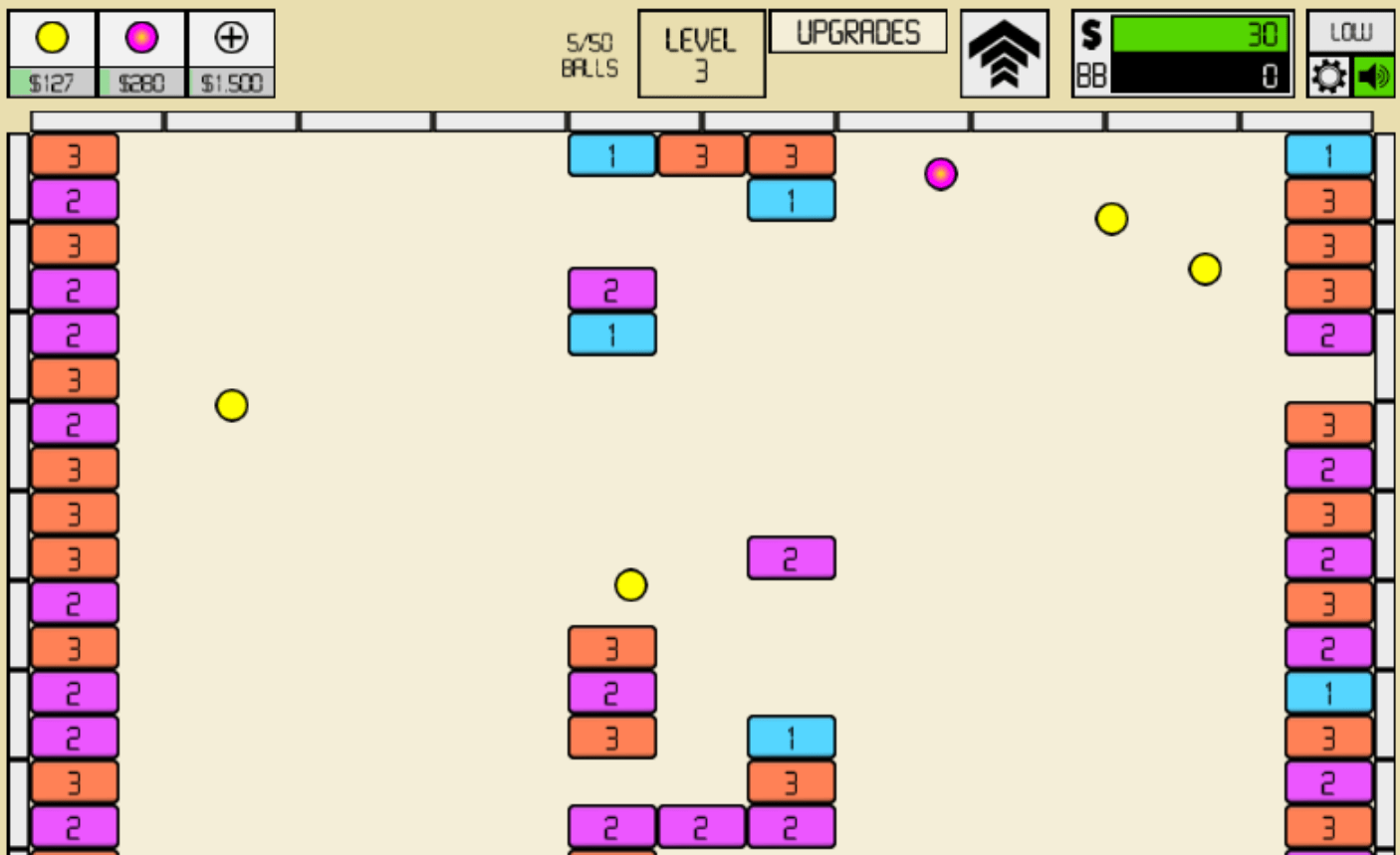
Idle Breakout is the ideal game for those who want something relaxing and low-maintenance to play as you don’t have to intervene often to score well. It takes the form of a classic brick-breaker game, but the user can also click bricks to destroy them and accumulate points to purchase balls. These balls then automatically bounce around the screen and destroy the bricks, which generates further points players can use to upgrade or increase their balls. The key to success in this game is deciding which upgrades are the most efficient.

Fundamentally this comes down to the idea of opportunity cost – the benefit you forego in choosing one course of action over another. The player needs to decide which of these upgrades will wield the highest return when applied to the game. This can be presented in the form of decision analysis, which uses utility functions to determine the relative value to the individual of each payoff. Although this is a somewhat advanced topic, it goes to show the versatility of idle games and their utility in teaching mathematical concepts.

Thinking Mathematically

Problem-solving permeates the mathematics curriculum from Key Stage 1 to Key Stage 5 and beyond. Arguably, being able to think mathematically and solve problems has become one of the most important skills our students need to master. There are several strategies in Mathematics that help in problem-solving; training the mind to think in this way can greatly enhance decision-making skills. Thinking mathematically does not entail knowing the great formulae and methods of mathematics, but just being logical and applying common sense.

This is where games such as Idle Toy Factories find their niche as they rely heavily on decision-making, strategic thinking, and logic to be highly successful. Players start by manually clicking on a button to create rubber ducks. When the toy is created, players earn money for their products. Players then need to make a series of decisions to progress the factory, including when to upgrade. They need to weigh whether upgrades are financially viable and whether they are worth waiting for.

Teaching the Fundamentals of Probability

Idle Dice is perfect for when you feel like playing a game without putting too much effort into it. The aim is to score as many points as possible from rolling dice, which can be done through a click or automatically. Each dice can be upgraded with multipliers using the points, or more dice can be bought and rolled simultaneously with the original. Although there is a strategy to Idle Dice, there is also the underlying concept of probability and the impact this has on scores and the rate at which dice can be improved.

This game can be used to initially display the probability of each number when rolling one dice. The expected probability for each number on the dice is 1/6 but students could record the outcomes of rolling the dice x times and then calculate the relative frequency of each outcome. This can also link to testing whether a dice is likely to be biased or not. As students increase the number of dice in the game, they will soon realize that some outcomes happen more than others. Each outcome has a  1/36 chance of appearing but there are now multiple ways to get certain totals from two dice. This information can then be used to help students decide which upgrades are going to have the most impact on their score, which they need to maximize to buy further upgrades.

Check out our recommendations for the best idle games – you might learn a thing or two!